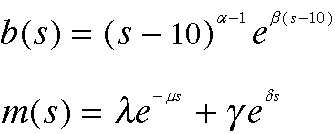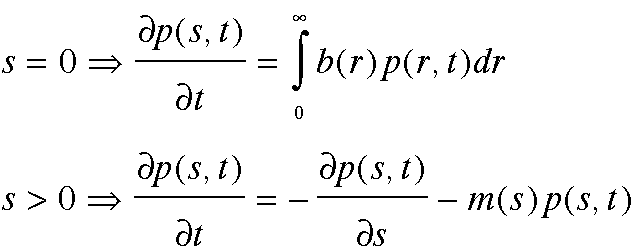
Let p(s,t) be the population of age s at time t. Let the function b(s) be the birth rate of people aged s, and let m(s) be their death rate. Then the dynamics of the population are described by the partial differential equation (PDE) displayed below. The first line of the PDE gives the birth process, i.e. the arrival of newly born infants (age s = 0) at time t. The second line of the PDE gives the aging and death process at time t for every age s > 0.
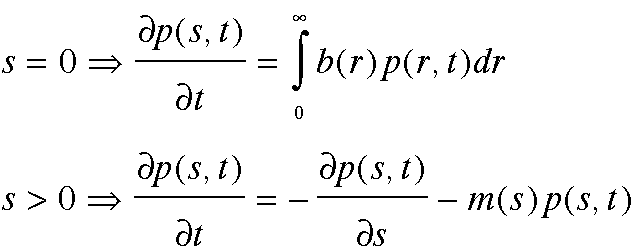
The simulation model used a gamma distribution for the age-specific birth rates, shifted so as to start at 10 years of age, and a sum of two exponentials for the age-specific mortality rates. The first term in the mortality function is the infant mortality curve, and the second term describes the exponentially increasing adult mortality with increasing age.